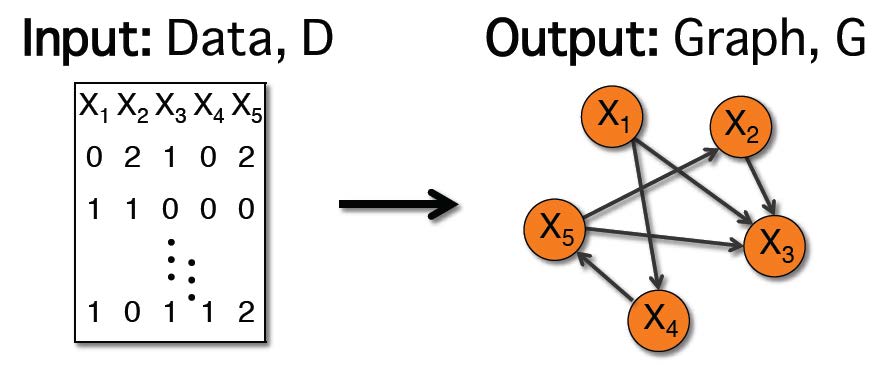
Bayesian networks are graphs that represent probabilistic relationships between variables. Learning the graph structure that best fits the data is often framed as an optimization problem, where the search space is the set of all possible graph structures, and the objective function has some measure of nearness to the data, as well as some regularization term to avoid overly dense structures. Since this problem is well-known to be NP-hard, research has traditionally focused on developing various heuristic search strategies. Recent work by Brenner and Sontag, 2013, has taken a different approach, developing a new objective function, called SparsityBoost. SparsityBoost looks for strong evidence in the data that an edge should not be present in the optimal graph, and boosts the score for graphs that are consistent with this evidence. The original presentation was only for binary variables. Here, I show how the score can be extended to networks over discrete variables with arbitrary numbers of states, and evaluate accuracy and efficiency as compared with the use of more traditional scoring functions.
My longer term goal is to use probabilistic graphical models to study cystic fibrosis (CF), the most common life-shortening genetic disease in Caucasians. I am working to develop structure learning algorithms which will be able to incorporate various kinds of data that are available on CF, for example to build a CF gene regulatory network.