Members: Teresa Huang, Zacharie Martin, Greg Scanlon, Eva Wang Mentors: Soledad Villar, David W. Hogg
Abstract
Recent work has shown that neural networks are susceptible to adversarial attacks, but what about simpler machine learning models? In this paper we investigate adversarial attacks to popular machine learning models for regressions in astronomical data. Namely, AstroNN (a Bayesian Neural Network), The Cannon (a quadratic generative model), and a simple linear regression. We suggest a few approaches to measuring the strength of adversarial attacks that take into consideration the physical properties of predictions. Our results suggest that generative (or causal) models are more robust to adversarial attacks than discriminative models.
Introduction
Adversarial attack in image classification: a small amount of noise added to a data point that results in the model assigning the incorrect class label with high confidence
- In physical sciences, deep learning as well as other classical methods are being successfully used for regressions
- A method’s vulnerability to attack may be indicative of some kind of deficiency in the size or coverage of the training data
- Our work investigates the susceptibility of different classes of astronomical regression models to adversarial attacks

X
“panda”
57.7% confidence


Methodology
Data
- Our data are stars which are described by their spectra and
- derived labels from the APOGEE Data Release (DR14)
- 1,000 spectra are randomly selected using the same preprocessing as targeted models to ensure compatibility
Models
There are many different kinds of regressions in the field of
astrophysics that could be targets for attack.
- Linear discriminative regressions
- Generative regressions
- Discriminate neural networks
How to find an attack
- Adversarial attack at the data point x is a perturbation ∆x∈ S that maximizes the loss:
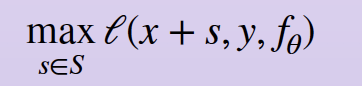
View Image Long Description
- There exist different strategies for finding the optimal perturbations. In our paper we focus on the Fast Gradient Sign Method (FGSM) from Goodfellow et al. (2014), which consists of one gradient step for the optimization function
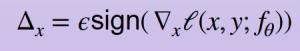
View Image Long Description
How to evaluate its success:
- Comparison between attacks and random perturbations
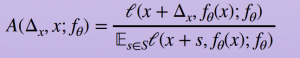
View Image Long Description
Results
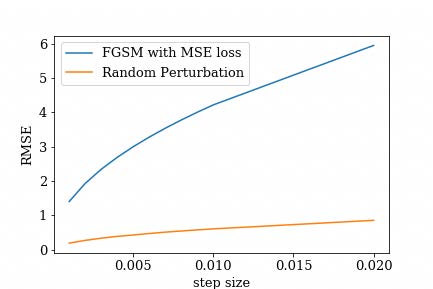
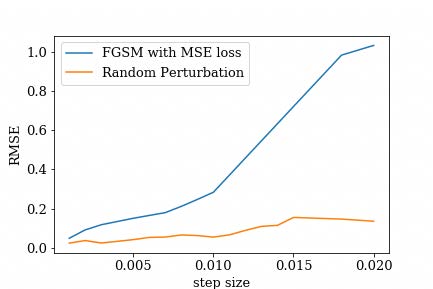
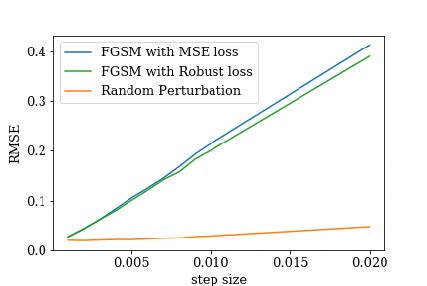
Root Mean Square Error (RMSE) loss between model output given random perturbations versus optimal FGSM perturbations
Linear Model
The Cannon
AstroNN
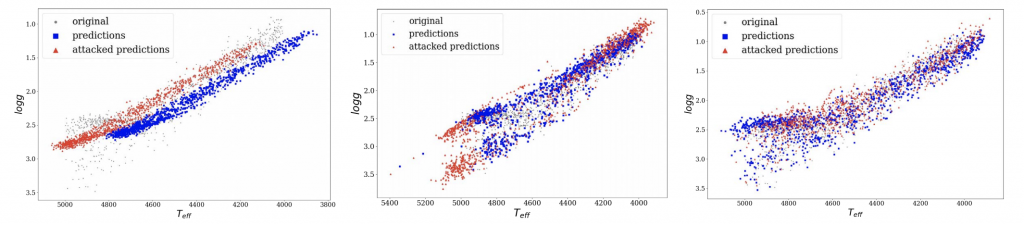
Model Predicted Labels, Attacked Labels and Ground Truth Labels
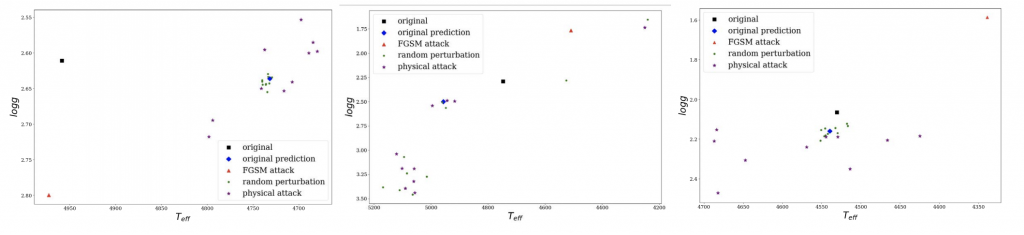
Output Label Space: examples of star 500 (left, Linear Model), star 758 (middle, the Cannon), star 244 (right, AstroNN)
Input Flux Space: original spectrum (left), added adversarial perturbation (middle), perturbed spectrum (right)

Discussion
In our experiments, we use the FGSM method with step size ranging from 0.001 to 0.02 and step value 0.01 (11 points in total). All three models use MSE as loss objective to calculate gradient direction for attacks.
- The first row of plots shows the RMSE loss for each model
- The second row of plots compares two labels predicted by the
- models without attack, predicted under attack and ground truth
- Highlights of attacks to individual stars are shown in the third row: points illustrate attacked predictions, random perturbations, original predictions, ground truth labels, and physical model attacks
- To confirm the adversarial attacks are small and uninformative, the fourth row shows one example flux spectrum. We can see the perturbation is adding random small noises to each flux pixel, almost imperceptible for human eyes
To compare the susceptibility of each model to adversarial attacks we measure each model’s sensitivity quotient, defined as:

View Image Long Description
At the step size of interest 0.01, we observe the linear model’s sensitivity quotient is 6.92, The Cannon is 4.50 and AstroNN is 6.93. The Cannon is therefore more robust to adversarial attacks than the linear model and AstroNN as measured by the SQ.
