On this page: Overview • Fall 2024 Capstone Project List • 2023 Posters • Best Fall 2023 Capstone Posters • Best Fall 2023 Student Voted Posters • Best Fall 2023 Student Voted Runner-Up Posters • Fall 2023 Capstone Project List
Overview

CDS master’s students have a unique opportunity to solve real-world problems through the capstone course in the final year of their program. The capstone course is designed to help students apply their knowledge to practical situations and develop critical skills such as problem-solving and collaboration.
Students are matched with research labs within the NYU community and industry partners to investigate pressing issues, applying data science to the following areas:
- Probability and statistical analyses
- Natural language processing
- Big Data analysis and modeling
- Machine learning and computational statistics
- Coding and software engineering
- Visualization modeling
- Neural networks
- Signal processing
- High-dimensional statistics
Capstone projects provide students with the opportunity to work in their field of interest and gain exposure to applicable solutions. Project sponsors, NYU labs, and external partners benefit from having a fresh perspective applied to their projects.
“Capstone is a unique opportunity for students to solve real-world problems through projects carried out in collaboration with industry partners or research labs within the NYU community,” says capstone advisor and former CDS Research Fellow Anastasios Noulas. “It is a vital experience for students ahead of their graduation and prior to entering the job market, as it helps them improve their skills, especially in problem-solving contexts that are atypical compared to standard courses offered in the curriculum. Cooperation within teams is another crucial skill built through the Capstone experience as projects are typically run across groups of 2 to 4 people.”
The Capstone Project offers organizations the chance to propose a project that our graduate students will work on as part of their curriculum for one semester. Information on the course, along with a questionnaire to propose a project, can be found on the Capstone Fall 2025 Project Submission Form.
If you have any questions, please reach out to ds-capstone@nyu.edu.
Fall 2024 Capstone Project List
- A machine learning framework for identifying interacting DNA elements from multiomics data
- A Non-biased Resume Screener in the Public Interest
- Advanced AI Techniques for Dynamic Portfolio Management and Financial Forecasting
- AI Tools for Journalists
- AI-Driven Reimbursement Code Discovery for HealthTech Start-Ups
- AI-powered deconvolution of RNA-sequencing data data
- American Colleges and Universities As Social Networks
- Audio-Visual Speaker Diarization Leveraging Foundation Models
- Calculating Weights for Causal Inference using Wasserstein GANs
- Deep learning models for cryptocurrency price analysis
- Designed Validation Sets
- Detecting Cognitive Impairment in Patient-Provider Communication
- Developing Multimodal Detection Systems for Narratives Promoting Misleading Information
- Developing Real-Time World Insight Reports with Machine Learning and LLMs
- Digitizing P&ID into Industrial Knowledge Graphs
- Dual-RAG: Advanced Financial Video QA with Multimodal RAG system
- Enhanced Automatic Annotation of Spoken Adult-Child Interactions
- Enhancing Large Language Models for Psychiatric Assessment
- Estimation of a Latent Space Model for Strategic Network Formation
- Hepatocellular Carcinoma Recurrence Prediction Radiomics Model
- Improving genetic prediction of disease risk
- Improving MRI Image Reconstruction via Generative AI
- Information-constrained emergent communication
- Large Language Models Encode Search for Clinical Evidence in Cancer Therapeutics
- Learning to detect breast cancer utilizing all imaging modalities
- Life Time Value (LTV) Model
- Long-form Egocentric Video Understanding
- Machine Learning-Driven Performance Monitoring in NYU’s DWDM Optical Transport Network
- Model and predict videoconference communication experience quality using multimodal data
- Optimizing Generative AI Modeling Stack for Sophisticated Financial Question Answering
- Optimizing Kidney Composite Allocation Score Using Simulation Optimization
- Political Partisanship and the US Judicial System
- Power Grids and Markets: Quantitative Trading and Analysis
- Predicting Agency Project/Program Success
- Real-Time Interpretation and Translation for Low-Resource Languages
- Relational Deep Learning and Graph Neural Networks for Anti Money Laundering
- Scaling Satellite Imagery of Urban Streets via Automated Classification and OpenStreetMap
- Solar Foundation Models
- Spatial Morbidity and Co-morbidity in the U.S.
- Tofu’s Candidate Matching Model
- Understanding Distribution Shifts in Time
- Use AI and math tools to do real estate appraisals
- User-centric AI-models for assisting the visually impaired
- Utilize large language model to analyze radiology report
- Video representation learning
*Best Fall 2024 Posters Coming Soon
2023 Posters
Best Fall 2023 Capstone Posters
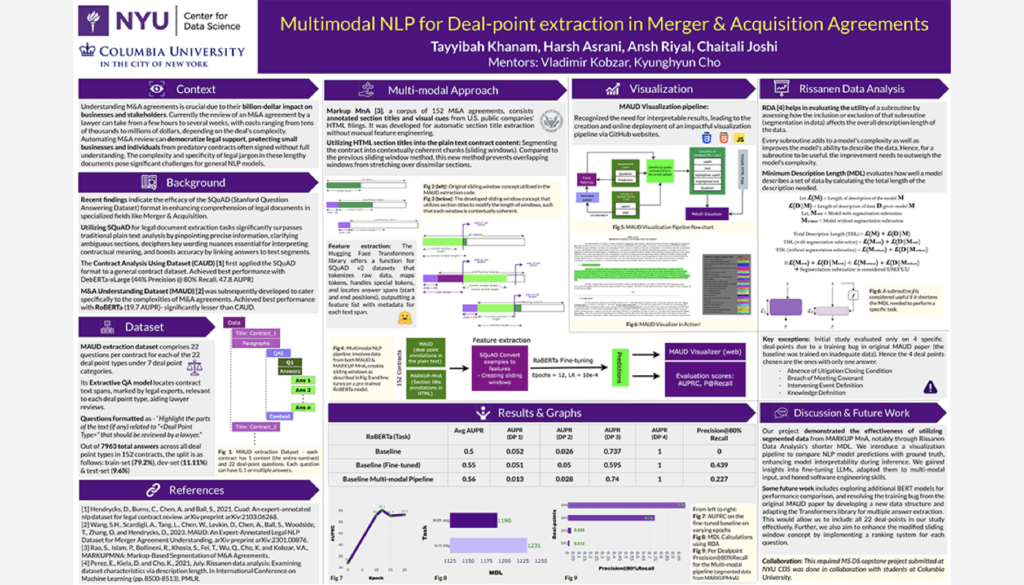
Multimodal NLP for M&A Agreements
Student Authors: Harsh Asrani, Chaitali Joshi, Tayyibah Khanam, Ansh Riyal | Project Mentors: Vlad Kobzar, Kyunghyun Cho
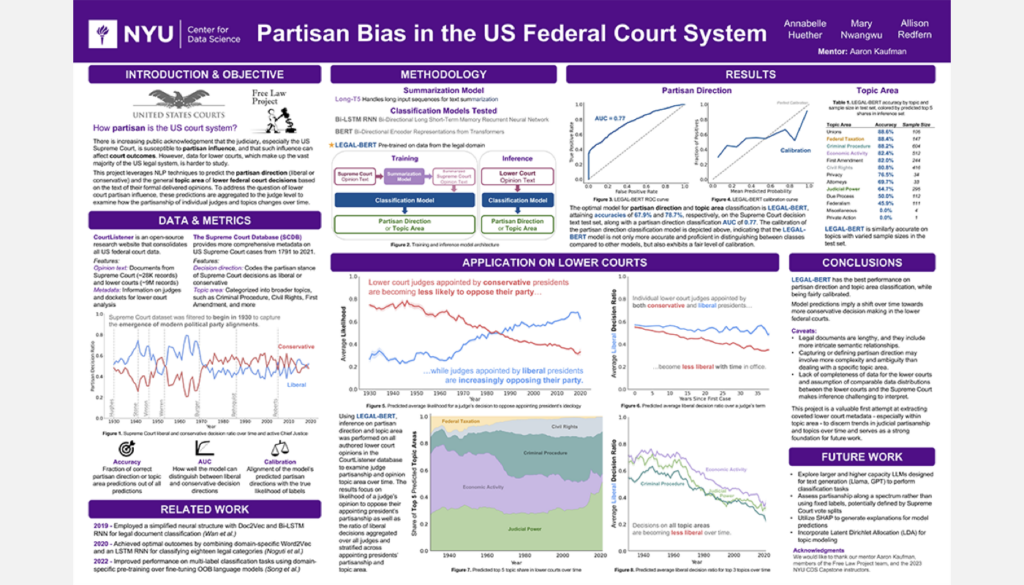
Partisan Bias and the US Federal Court System
Student Authors: Annabelle Huether, Mary Nwangwu, Allison Redfern | Project Mentors: Aaron Kaufman, Jon Rogowski
Best Fall 2023 Student Voted Posters
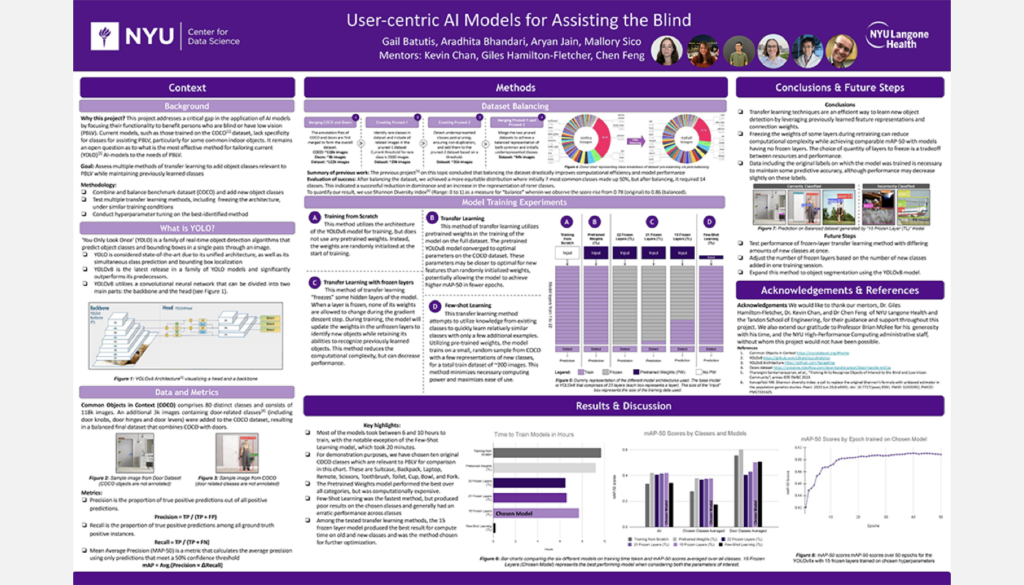
User-Centric AI Models for Assisting the Blind
Student Authors: Gail Batutis, Aradhita Bhandari, Aryan Jain, Mallory Sico | Project Mentors: Giles Hamilton-Fletcher, Chen Feng, Kevin C. Chan

Multi-Modal Foundation Models for Medicine
Student Authors: Yunming Chen, Harry Huang, Jordan Tian, Ning Yang | Project Mentors: Narges Razavian
Best Fall 2023 Student Voted Runner-Up Posters
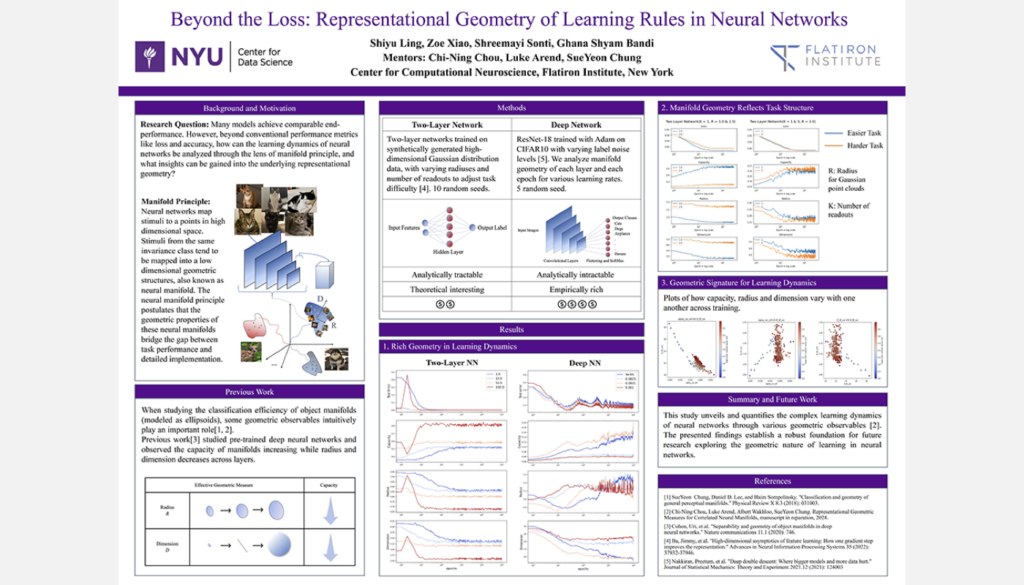
Representational Geometry of Learning Rules in Neural Networks
Student Authors: Ghana Bandi, Shiyu Ling, Shreemayi Sonti, Zoe Xiao | Project Mentors: SueYeon Chung, Chi-Ning Chou

Medical Data Leakage with Multi-site Collaborative Training
Student Authors: Christine Gao, Ciel Wang, Yuqi Zhang | Project Mentors: Qi Lei
Fall 2023 Capstone Project List
- A machine learning model to predict future kidney function in patients undergoing treatment for kidney masses
- Advanced Name Screening and Entity Linking Using large language models
- Automated assessment of epilepsy subtypes using patient-generated language data
- Bringing Structure to Emergent Taxonomies from Open-Ended CMS Tags
- Build Models for Multilingual Medical Coding
- Building an Interactive Browser for Epigenomic & Functional Maps from the Viewpoint of Disease Association
- Causal GANs
- Designing Principled Training Methods for Deep Neural Networks
- Developing predictive shooting accuracy metric(s) for First-Person-Shooter esports
- Discovering misinformation narratives from suspended tweets using embedding-based clustering algorithms
- Does resolution matter for transfer learning with satellite imagery?
- Egocentric video zero-shot object detection
- Evaluating the Capability of Large Language Models to Measure Psychiatric Functioning
- Explanatory Modeling for Website Traffic Movements
- Extracting causal political narratives from text.
- Fine-Tuning of MedSAM for the Automated Segmentation of Musculoskeletal MRI for Bone Topology Evaluation and Radiomic Analysis
- Foundation Models for Brain Imaging
- Housing Price Forecasting – Alternative Approaches
- Identify & Summarize top key events for a given company from News Data using ML and NLP Models
- Improving Out-of-Distribution Generalization in Neural Models for Astrophics and Cosmology?
- Knowledge Extraction from Pathology Reports Using LLMs
- Leverage OncoKB’s Curated Literature Database to Build an NLP Biomarker Identifier
- Measuring Optimizer-Agnostic Hyperparameter Tuning Difficulty
- Medical Data Leakage with Multi-site Collaborative Training
- Metadata Extraction from Spoken Interactions Between Mothers and Young Children
- Multi-Modal Foundation Models for Medicine
- Multimodal NLP for M&A Agreements
- Multimodal Question Answering
- Network Intrusion Detection Systems using Machine Learning
- Online News Content Neural Network Recommendation Engine
- OptiComm: Maximizing Medical Communication Success with Advanced Analytics
- Partisan Bias and the US Federal Court System
- Predicting cancer drug response of patients from their alteration and clinical data
- Predicting year-end success using deep neural network (DNN) architecture
- Prediction of Acute Pancreatitis Severity Using CT Imaging and Deep Learning
- Preparing a Flood Risk Index for the State of Assam, India
- Representational geometry of learning rules in neural networks
- Segmentation of Metastatic Brain Tumors Using Deep Learning
- Social Network Analysis of Hospital Communication Networks
- Supporting Student Success through Pipeline Curricular Analysis
- Transformers for Electronic Health Records
- Uncertainty Radius Selection in Distributionally Robust Portfolio Optimization
- Unveiling Insights into Employee Benefit Plans and Insurance Dynamics
- User-centric AI models for assisting the blind
- Using Deep Learning to Solve Forward-Backward Stochastic Differential Equations
- What Keeps the Public Safe While Avoiding Excessive Use of Incarceration? Supporting Data-Centered Decision-making in a DA’s Office
